The map of nuclear deformation takes the form of a mountain landscape
30 December 2020
EurekAlert!: [https://www.eurekalert.org/pub_releases/2020-12/thni-tmo123020.php]
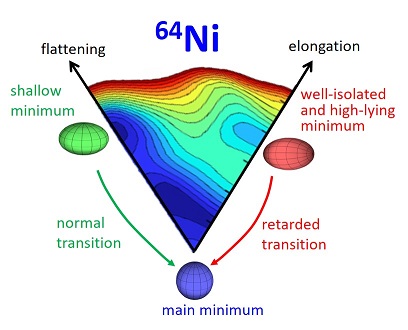
Deformation landscape of the nickel-64 nucleus. Prolate, oblate local minima and main spherical minimum are indicated by red, green and blue ellipsoids, respectively. (Source: IFJ PAN)
Until recently, scientists believed that only very massive nuclei could have excited zero-spin states of increased stability with a significantly deformed shape. Meanwhile, an international team of researchers from Romania, France, Italy, the USA and Poland showed in their latest article that such states also exist in much lighter nickel nuclei. Positive verification of the theoretical model used in these experiments allows describing the properties of nuclei unavailable in Earth laboratories.
More than 99.9 per cent of the mass of an atom comes from the atomic nucleus, the volume of which is over a trillion times smaller than the volume of the entire atom. Hence, the atomic nucleus has an amazing density of about 150 million tons per cubic centimetre. This means that one tablespoon of nuclear matter weighs almost as much as a cubic kilometre of water. Despite their very small size and incredible density, atomic nuclei are complex structures made of protons and neutrons. One may expect that such extremely dense objects would always take spherical form. In reality, however, the situation is quite different: most nuclei are deformed – they exhibit shape flattened or elongated along one or even two axes, simultaneously. To find the favourite form of a given nucleus, it is customary to construct a landscape of the potential energy as a function of deformation. One may visualize such landscape by drawing a map on which the plane coordinates are the deformation parameters, i.e. degrees of elongation or flattening along the two axes, while the colour indicates the amount of energy needed to bring the nucleus to a given shape. Such a map is a full analogy to a geographical map of mountain terrain.
If a nucleus is formed in the nuclear reaction, it appears at a given point of the landscape – it takes specific deformation. It then starts to slide (change deformation) towards the lowest energy point (stable deformation). In some cases, however, before reaching the ground state, it may be stopped for a while in some local minimum, a trap, which corresponds to metastable deformation. This is very similar to water that springs in a particular location in the mountain area and flows downward. Before it reaches the lowest valley, it may be trapped in local depressions for some time. If a stream connects the local depression to the lowest point of the landscape, water will flow down. If the depression is well isolated, the water will stay there for a very long time.
Experiments have shown that local minima in the nuclear deformation landscape at spin zero exist only in massive nuclei with atomic numbers larger than 89 (actinium) and a total number of protons and neutrons well above 200. Such nuclei can be trapped in these secondary minima at metastable deformation for a period even tens of millions of times longer than the time needed to reach the ground state without being slowed down by the trap. Until a few years ago, an excited zero-spin state associated with metastable deformation had never been observed among nuclei of lighter elements. The situation changed a few years ago when a state with sizeable deformation characterized by increased stability was found in nickel-66, the nucleus with 28 protons and 38 neutrons. This identification was stimulated by calculations performed with the sophisticated Monte Carlo shell model developed by Tokyo University theorists, which predicted this deformation trap.
“The calculations performed by our Japanese colleagues also provided another unexpected result
”, says Prof. Bogdan Fornal (IFJ PAN). “They showed that a deep, local depression (trap) associated with sizeable deformation should be present also in the potential energy landscape of nickel-64, the nucleus with two neutrons less than nickel-66, which until now was considered to have only one main minimum with a spherical shape. The problem was that in nickel-64 the depression was predicted at high excitation energy – at high altitude in the mountain terrain analogy – and it was extremely difficult to find an experimental method to place the nucleus in this trap.
”
A tour de force took place involving four complementary experiments, jointly conducted by a collaboration lead by experimentalists from Romania (IFIN-HH in Bucharest), France (Institut Laue-Langevin, Grenoble), Italy (University of Milan), USA (the University of North Carolina and TUNL) and Poland (IFJ PAN, Krakow). Measurements were performed at four different laboratories in Europe and the USA: Institut Laue-Langevin (Grenoble, France), IFIN-HH Tandem Laboratory (Romania), Argonne National Laboratory (Chicago, USA) and the Triangle Universities Nuclear Laboratory (TUNL, North Carolina, USA). Different reaction mechanisms were employed including proton and neutron transfer, thermal-neutron capture, Coulomb excitation and nuclear-resonance fluorescence, in combination with state-of-the-art gamma-ray detection techniques.
All the data taken together allowed to establish the existence of two secondary minima in the potential energy landscape of nickel-64, corresponding to oblate (flattened) and prolate (elongated) ellipsoidal shapes, with the prolate one being deep and well isolated as indicated by the significantly retarded transition to the main spherical minimum.
"The extension of time which the nucleus spends when trapped in the prolate minimum of the Ni-64 nucleus is not as spectacular as that of the heavy nuclei, where it reaches tens of millions of times. We recorded the increase of only a few tens of times; yet the fact that this increase is close to the one provided by the new theoretical model, is a great achievement
”, states Prof. Fornal.
A particularly valuable outcome of the study is identifying a previously unconsidered component of the force acting between nucleons in complex nuclear systems, the so-called tensor monopole, which is responsible for the multifaceted landscape of deformation in the nickel isotopes. Scientists expect that this interaction is accountable to a large extent for shaping the structure of many nuclei that have not yet been discovered.
In a broader perspective, the presented investigation indicates that the theoretical approach applied here, being able to adequately predict the unique characteristics of the nickel nuclei, has great potential in describing the properties of hundreds of nuclear systems which are not accessible in the laboratory on the Earth today, but continually produced in stars.
[PDF]
Contact:
Prof. Bogdan Fornal
The Institute of Nuclear Physics, Polish Academy of Sciences
tel. +48 12 662 8200
email: bogdan.fornal@ifj.edu.pl
Scientific papers:
N. Mărginean, D. Little, Y. Tsunoda, S. Leoni, R. V. F. Janssens, B. Fornal, T. Otsuka, C. Michelagnoli, L. Stan, F. C. L. Crespi, C. Costache, R. Lica, M. Sferrazza, A. Turturica, A. D. Ayangeakaa, K. Auranen, M. Barani, P. C. Bender, S. Bottoni, M. Boromiza, A. Bracco, S. Călinescu, C. M. Campbell, M. P. Carpenter, P. Chowdhury, M. Ciemała, N. Cieplicka-Oryńczak, D. Cline, C. Clisu, H. L. Crawford, I. E. Dinescu, J. Dudouet, D. Filipescu, N. Florea, A. M. Forney, S. Fracassetti, A. Gade, I. Gheorghe, A. B. Hayes, I. Harca, J. Henderson, A. Ionescu, Ł. W. Iskra, M. Jentschel, F. Kandzia, Y. H. Kim, F. G. Kondev, G. Korschinek, U. Köster, Krishichayan, M. Krzysiek, T. Lauritsen, J. Li, R. Mărginean, E. A. Maugeri, C. Mihai, R. E. Mihai, A. Mitu, P. Mutti, A. Negret, C. R. Niţă, A. Olăcel, A. Oprea, S. Pascu, C. Petrone, C. Porzio, D. Rhodes, D. Seweryniak, D. Schumann, C. Sotty, S. M. Stolze, R. Şuvăilă, S. Toma, S. Ujeniuc, W. B. Walters, C. Y. Wu, J. Wu, S. Zhu, and S. Ziliani
„Shape Coexistence at Zero Spin in 64Ni Driven by the Monopole Tensor Interaction”
Phys. Rev. Lett. 125, 102502;
DOI: 10.1103/PhysRevLett.125.102502
Images:
Deformation landscape of the nickel-64 nucleus. Prolate, oblate local minima and main spherical minimum are indicated by red, green and blue ellipsoids, respectively. (Source: IFJ PAN)