From cathedral floors to transistor circuits: The splendid generative potential of the Sierpinski triangle

13 December 2018

EurekAlert!: [https://www.eurekalert.org/pub_releases/2018-12/thni-tsg121318.php]

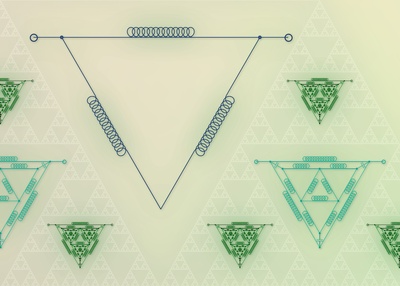
Three iterations of simple electronic oscillators. The Sierpinski triangle is visible in the background. (Source: IFJ PAN)

One transistor, just a pair of inductors and capacitors. Such a simple electronic circuit can become an oscillator with a surprising richness of behavior. However, even more interesting effects become visible if the structure of connections is fractal and shows some... imperfections. Could similar rules explain the diversity and complexity of the human brain dynamics?

Intuition suggests that self-similarity appears only in systems as complex as neural networks in the brain, or in fascinating shapes of nature, for example in the famous Romanesco broccoli buds. At the Institute of Nuclear Physics of the Polish Academy of Sciences (IFJ PAN) in Cracow a discovery was made that in some ways challenges this belief. In close collaboration with colleagues from the University of Catania and the University of Trento in Italy, the researchers constructed an elementary electronic oscillator based on just one transistor. As it turns out, when it contains fractal arrangements of inductors and capacitors, these generate amazingly rich characteristics of the electrical signals.

Even when we may not pay attention to it, we are surrounded by objects whose shape has a remarkable property: it is similar regardless of how close or far we look. The whole is sometimes similar to its parts! This extraordinary feature, known as self-similarity, is a distinguishing property of mathematical fractals. Self-similarity, however, is not only the domain of mathematics. It is readily detectable, for example, in the shapes of clouds, coastlines, in the structure of plants or even in ourselves. Fractal properties are visible in the arrangement of the bronchi in the lungs, blood vessels in the brain, and, at a smaller scale, in the layout of dendrites and in the connections between neurons in the brain.

Why fractals seem to arise so pervasively? Scientists from all disciplines have long been fascinated by this profound question. But it is only more recently that engineers have started taking an interest in them for practical applications. What they like is that fractals can fold very long lines into small areas, helping the miniaturisation of antennas. Notwithstanding, it is possible to build fractal circuits quite simply, just by connecting together standard inductors and capacitors according to a fractal pattern. Regardless of their physical size, such circuits would always have a self-similar shape – and interesting properties. But so far nobody has examined how they could perform when inserted into an oscillator.

“In our latest research, we started off from an extremely simple circuit that we had discovered last year. It is really tiny, as it only includes one transistor, two inductors, one capacitor and one resistor. Nevertheless, depending on the geometry of the connections and parameters of the inductors and capacitors, the circuit exhibits various, sometimes very complex activities. We wondered what would happen if we replaced the inductors with smaller and smaller self-similar circuits” says Dr. Ludovico Minati (IFJ PAN), the main author of the paper in the renowned scientific journal Chaos.

There are many patterns which can be repeated to generate fractals. One of the simplest ones starts off drawing a triangle, then taking the mid-points of its sides and connecting them. In this way, four smaller triangles are formed: three at the vertices and one in the middle. Then, the triangle in the middle should be ignored, and the algorithm should be iterated in the other triangles. A large number of these iterations leads to the formation of the Sierpinski triangle, from the name of a Polish mathematician who studied its remarkable properties. However, it has, in fact, been well known for centuries as a decorative element and appears quite frequently in the floors of churches in the Lazio region of Italy, realised in the medieval period by the Marmorari Romani.

Intrigued by the idea of transforming the analyzed circuit into a fractal, the Cracow researchers attempted to recreate patterns of the Sierpinski triangle with inductors and capacitors. And here a surprise awaited them. Although the circuits for laboratory tests were realized with the highest precision, the generated patterns failed to reach the same heights of complexity and aesthetic beauty that was observed in simulations!

As one considers just a triangle of inductors, the generated signals are not so complex. But as one inscribes more and more triangles, increasing the depth of the fractal (meaning, how many nested levels, or iterations, are present), what is found is that the signals become more and more intricate, delineating a motion in as many as... ten dimensions! However, when one goes from numerical simulations to building the real circuits, at first the reality seems more bleak, since such a level of dynamical richness is not reached, and the number of dimensions decreases. It turns out that this is due to the fact that real components are not “ideal”, effectively making the fractal more blurred.

“At first, we were quite disappointed. Later, we discovered something even more interesting than what we had initially planned to study. The key to remove the hindreance caused by the non-ideal elements was not to unblur the fractal structure, but to... damage it!” adds Dr. Minati, still looking somewhat surprised.

Like artists of all walks like to say, there is beauty in imperfection, and the study of Cracow researchers seems to firm up this statement. By damaging the fractals slightly, for example, by removing some components or inserting some short-circuits, it is possible to obtain much more complex resonances, which are readily confirmed by the experiment. In fact, it turns out that these are rather similar to what would be obtained by reshuffling all components in a completely random manner. In a real, physically-built circuit, these more complex resonances give back what was lost due to the non-ideal components, offering new ways of obtaining complex signals.

“Perfection belongs to mathematics, and neither to biology nor physics. Most of the fractals we observe in nature are not perfect at all, and we usually take this fact as an obvious flaw. Meanwhile, our understanding of the consequences of imperfections may be quite limited,” notes Prof. Stanislaw Drozdz (IFJ PAN, Cracow University of Technology).

The latest research shows that in simple, fractal electronic oscillators, imperfections in the structure of connections radically increase the dynamics of behavior. This result of Cracow physicists even provokes some speculations related to the structure and functions of the human brain.

“We might be tempted to assume that imperfections in the layout of neural connections arise accidentally in a process of brain growth from a structure that would otherwise be ideal by definition. In fact, this is probably not the case and their presence may serve a specific purpose and be a result of long-term natural selection. Neural networks with defects will manifest more complex dynamics! Who knows, then, if inspired by this observation, one day we will even intentionally build imperfect computers?” sums up Prof. Drozdz.

[PDF]

Contact:

Dr. Ludovico Minati
The Institute of Nuclear Physics Polish Academy of Sciences
tel. +48 12 662 8241
email: ludovico.minati@ifj.edu.pl

Prof. Stanisław Drożdż
The Institute of Nuclear Physics Polish Academy of Sciences
tel. +48 12 662 8220
email: stanislaw.drozdz@ifj.edu.pl

Scientific papers:

„High-dimensional dynamics in a single-transistor oscillator containing Feynman-Sierpiński resonators: Effect of fractal depth and irregularity”
L. Minati, M. Frasca, G. Giustolisi, P. Oświęcimka, S. Drożdż, L. Ricci
Chaos 28, 093112 (2018)
DOI: 10.1063/1.5047481

Images:

Three iterations of simple electronic oscillators. The Sierpinski triangle is visible in the background. (Source: IFJ PAN)

Real electronic oscillators generate more complex dynamics as a result of imperfections in fractal connections. (Source: IFJ PAN)

Three iterations of simple electronic oscillators. The Sierpinski triangle is visible in the background. (Source: IFJ PAN)