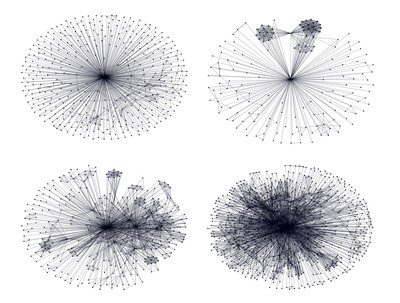
What sort of stream networks do scientific ideas flow along?

10 January 2018

EurekAlert!: [http://www.eurekalert.org/pub_releases/2018-01/thni-wso011118.php]

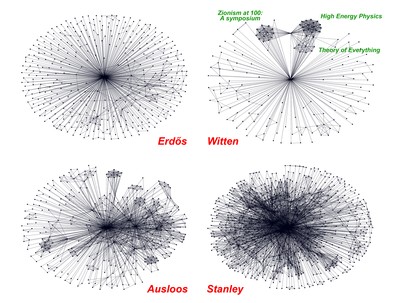
Graph showing the flow of ideas initiated by Prof. H. Eugene Stanley. Connections between collaborators show the existence of several clearly visible sub-networks, corresponding to scientific communities focusing on specific research topics. (Source: IFJ PAN)

When scientists have an interesting idea, the result is usually a joint publication. At the Institute of Nuclear Physics of the Polish Academy of Sciences in Cracow, it has been shown that tracking the dependencies between co-authors, one can not only see the paths along which scientific ideas flow, but also reconstruct the structure of scientific cooperation and detect emerging communities. Interestingly, the proposed method of analysis can be an effective tool to fight terrorists and... dishonest politicians.

Panta rhei, everything flows. If Heraclitus of Ephesus was correct, not only rivers, but also ideas should flow. Tracking the flow of ordinary ideas can be difficult. In the case of scientific ideas, it is much easier: the researchers exchanging them usually produce joint publications. A group of researchers from the Institute of Nuclear Physics of the Polish Academy of Sciences (IFJ PAN) in Cracow, headed by Prof. Stanisław Drozdz (IFJ PAN, Cracow University of Technology), has analyzed the structures of links between the coauthors of scientific works forming around such eminent figures of modern science as Harry Eugene Stanley or Edward Witten. Illustrated in the form of graphs, the research results give a unique insight into the various forms of modern scientific cooperation.

“More and more people are now participating in scientific projects, and science itself is becoming more and more interdisciplinary. The scale of difficulty of the scientific issues under research is increasing, and we are also dealing with the rapid development of modern methods of communication. All this means that the links between scientists today have not only a significant complexity, but also constantly growing dynamics”, says Prof. Drozdz.

When starting to analyze the structures of scientific cooperation, the Cracow researchers made use of an idea connected with the figure of Paul Erdos, one of the greatest mathematicians of the twentieth century. Erdos was the author and co-author of approx. 1500 publications, with a total of over 500 people working together. Erdos' exceptional scientific activity provoked mathematicians to invent Erdos numbers, reflecting the scientific ‘kinship’ of a given person with Erdos himself. According to the definition, Erdos was assigned the number 0, the scientist who wrote the publication with him – 1, the scientist who wrote a publication with a person having an Erdos number of 1 – the number 2, etc.

“Our idea was to analyze the scientific connections of several contemporary outstanding scholars in a similar way and to present them in the form of graphs, or sets of nodes and lines connecting them. Naturally, the central node of each graph was a scientist chosen by us; the remaining nodes corresponded to his next, closer or further associates. In this approach, the connections between nodes can be interpreted as flows of ideas resulting in writing a joint publication”, explains Prof. Drozdz.

The simplest graph produced according to the above principles would be a graph for Paul Dirac, an English physicist-theoretician who always published his works as the sole author. Dirac's graph would therefore consist of just one node. There would be an equally uninteresting topology in graphs of modern scientific ventures in which hundreds of scientists participate, assigned to many subsequent publications in an often purely administrative manner (this is a common situation in the case of complex, long-term experiments, such as LHC and LIGO gravitational wave detectors). These graphs would consist of a large number of nodes, most of them connecting with all the others. The network of connections here is so dense that it is difficult to find any interesting dependencies.

The graph of Erdos himself also turned out to be moderately interesting: numerous links radiate from the central node to many neighboring nodes, and almost always ended there. Only some of the nodes symbolizing Erdos' associates were connected to each other. The shape of the structure was probably influenced here by the fact that the communication tools existing in the 20th century were much more poorly developed than at present and it was much more difficult for many scientists, especially the lesser known ones, to establish new contacts.

“When Erdos was dealing with the mathematical description of networks reflecting human interactions, he predicted that the connection structure would be quite democratic: most nodes would be in direct contact with a comparable, though not very large, number of other nodes. But at the turn of the century, for the first time, a large network was visualized: the Internet. Suddenly, it turned out that this network has a much less democratic structure: only 20% of nodes have access to 80% of connections. We discovered a self-organization resulting from the operation of a similar power law in the network of Professor Stanley”, notes Prof. Drozdz.

Prof. H. Eugene Stanley is an interdisciplinary statistical physicist, co-author of several dozen publications a year. His Hirsch index, reflecting the number and response of scientific publications, is one of the highest in the natural and technical sciences. In the idea flow network surrounding Stanley there are many highlighted nodes, around which there are more nodes, representing scientists developing their own research, and inspired by Stanley's works. Some of them, corresponding to such figures of science as Marcel Ausloos, Shlomo Havlin or Sergey Buldyrev, influenced their colleagues in a similarly creative way, focusing their own communities around themselves. As a result, the Stanley network acquired hierarchical features, in many places demonstrating the self-similarity characteristic of fractal objects.

The hierarchy of the ideas network is neither a universal feature nor is it characteristic of the outstanding figures of today's science. The graph illustrating the scientific connections of Edward Witten, a well-known mathematical physicist developing string theory, turned out to have a general outline resembling a simple star, as was so clearly visible in Erdos's graph. In Witten's, however, the presence of several distinct sub-structures separated from each other is visible. They correspond to communities dealing with specific topics, e.g. the theory of everything or the physics of high energies.

“The mathematical procedure proposed by us makes it possible to detect links between people which are not always perceived at first glance. The existence of some communities only became obvious when, constructing the graphs, we took into account the fact that connections between nodes can have different strengths. Some authors may, after all, publish joint works many times”, notes Prof. Drozdz.

In networks of interpersonal contacts, mathematics enables the revealing of the presence of communities connected by common ideas. The methods of analysis proposed by the Cracow physicists could thus be used for other purposes, e.g. to follow the structures of terrorist organizations. But it is possible to imagine other, more peaceful applications. For example, who knows if modern democracies would not function more effectively if, before elections, each of us could see a graph illustrating the network of the candidate's connections with other people next to his or her photo?

[PDF]

Contact:

Prof. Stanisław Drożdż
The Institute of Nuclear Physics of the Polish Academy of Sciences
tel. +48 12 6628220
email: stanislaw.drozdz@ifj.edu.pl

Scientific papers:

"Hierarchical organization of H. Eugene Stanley scientific collaboration community in weighted network representation"
S. Drożdż, A. Kulig, J. Kwapień, A. Niewiarowski, M. Stanuszek; Journal of Informetrics 11 (2017) 1114–1127
DOI: http://doi.org/10.1016/j.joi.2017.09.009

Images:

Graph showing the flow of ideas initiated by Prof. H. Eugene Stanley. Connections between collaborators show the existence of several clearly visible sub-networks, corresponding to scientific communities focusing on specific research topics. (Source: IFJ PAN)

annotations:

Graphs showing scientific connections initiated by Paul Erdos, Edward Witten, Marcel Ausloos and H. Eugene Stanley. In the case of Edward Witten there are three clearly visible sub-networks, corresponding to specific topics. (Source: IFJ PAN)